Trigonometry Formulas for Competitive Exams : In this article we are going to give important Trigonometry Formulas for competitive Exams.
All these Trigonometry Formula are important for any general exam like SSC Exams, Railway Exams, Bank Exams etc.
It is important to remember these Trigonometry Formulas for school exams and also many questions related to trigonometry are asked in SSC Exams, Railway Exams, Bank Exams etc. So if you are preparing for these exams then these Trigonometry Formulas for competitive exams are very useful for you.
In this article, we have given important Trigonometry Formulas for competitive exams which are equally useful for both school students and aspirants preparing for the competitive exams.
By remembering these Trigonometry Formulas for Competitive Exams, you can solved trigonometry related questions quickly. So remember all these Trigonometry Formulas for Competitive Exams given in this article.
Also read- >How to Prepare Current Affairs for One-day Exams like SSC, Bank, Railway >ST Inspector Salary as per 7th CPC, Job Profile and Promotion
Trigonometry Definition

Before knowing Trigonometry Formulas for Competitive Exams, you must know what is Trigonometry?
The word Trigonometry is derived from the Greek words Tri (meaning three) , “ gon” (meaning side) and ‘metron’ (meaning measure) .
The relationship between the sides and angles of a triangle is studied under trigonometry. Trigonometry has been used since ancient times. There is evidence of the use of trigonometry by the ancient Egyptians and Babylonians.
Ancient astronomers used trigonometry to measure the distances of stars and planets from Earth. Trigonometry is also used in today’s modern engineering and physical sciences.
Trigonometry Formulas for Competitive Exams
When we learn about Trigonometry Formula, we derive all the formulas for a right triangle only.
As you may know, a right-angled triangle has three sides – the base, the perpendicular and the hypotenuse.
As can be seen in the figure below, the horizontal side of the triangle is called the base. The side making an angle of 90° with the base is called Perpendicular and the other side opposite to 90° is called Hypotenuse.
Trigonometric Ratios
Trigonometric ratios are used to solve all problems related to trigonometry. These are also called Trigonometric Functions. These are the basic Trigonometry Formula.
There are 6 types of trigonometric ratios – Sine, Cosine, Tangent, Co-secant, Secant and Co-tangent. Their abbreviated forms are – sin, cos, tan, cosec, sec and cot.
Now we will find the trigonometric ratio on the basis of above given right angle.
First of all we will tell about Basic Trigonometry Formula, which are as follows
• sinθ = perpendicular / hypotenuse
• cosθ = base / hypotenuse
• tanθ= perpendicular / base
• cotθ = base / perpendicular
• secθ = hypotenuse / base
• coescθ = hypotenuse / perpendicular
These Trigonometry Formula is used when you know the length of the sides of a right angle triangle or know the length of one angle and one side and want to find the length of the other side.
Reciprocal Relations between Trigonometric Ratios
• sinθ = 1 / Cosecθ or Sin θ × Cosecθ = 1
• Cosecθ = 1 / sinθ or Cosecθ × Sin θ = 1
• Cosθ = 1 / Secθ or Cos θ × Sec θ = 1
• Secθ = 1 / Cosθ or Sec θ × Cos θ = 1
• Tanθ = 1 / Cotθ or Tan θ × Cot θ = 1
• Cotθ = 1 / Tanθ or Cot θ × Tan θ = 1
These Trigonometry Formula is used when the value of one trigonometric ratio is known and the value of the other trigonometric ratio is to be calculated. For example, if you know the value of cosec of an angle, then you can easily find the value of its sin.
Trigonometry Table
If you know the value of an angle of a triangle, then with the help of the trigonometry table given below, you can find the value of trigonometric ratios like sin, cos, tan, cosec, sec and cot.
You can solve most of the questions asked in the exam with the help of this table. So students are advised to memorize this table thoroughly along with Trigonometry Formula.
| who | 0° | 30° or π/6 | 45° or π/4 | 60° or π/3 | 90° or π/2 | 180° or π | 270° or 3π/2 | 360° or 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Trigonometric Identities or Pythagorean Identities
As you may know, an equation is said to be an identity if it is true for all values of the variables involved.
Similarly, an identity related to the trigonometric ratios of an angle is called a trigonometric identity. While this is true for all values of the corresponding angle(s).
These identities follow the Pythagorean Theorem, hence they are also called Pythagorean Identities. Now let us know what are the trigonometric identities –
• sin²θ + cos²θ = 1 • sin²θ = 1 – cos²θ • cos²θ = 1- sin²θ • Sec²θ – Tan²θ = 1 • 1 + tan²θ = sec²θ • Sec²θ –1 = Tan²θ • cosec²θ = cot²θ + 1 • sinθ = √ (1 – cos²θ) • cosθ = √( sinθ – 1 ) • tan²θ = sec²θ – 1 or tanθ = √(sec²θ – 1) • secθ = √(1 + tan²θ) • cosecθ = √(cot²θ + 1) • cot²θ = cosec²θ – 1 or cotθ = √ (cosec²θ – 1)
Trigonometric Ratios of Complementary Angles (Cofunction Identities)
Two angles of a triangle are said to be complementary angles when their sum equals 90 degrees.
| In radians | In degrees |
|---|---|
| sin (π/2 – θ) = cos θ | sin (90° – θ) = cos θ |
| cos (π/2 – θ) = sin θ | cos (90° – θ) = sin θ |
| tan (π/2 – θ) = cot θ | tan (90° – θ) = cot θ |
| cot (π/2 – θ) = tan θ | cot (90° – θ) = tan θ |
| sec (π/2 – θ) = cosec θ | sec (90° – θ) = cosec θ |
| cosec (π/2 – θ) = sec θ | cosec (90° – θ) = sec θ |
Periodicity Identities
We use these Trigonometry Formula to shift angles by π/2, π, 2π, 3π/2 etc.
Shifting by π/2
| In radians | In degrees |
|---|---|
| sin (π/2 + θ) = +cos θ | Sin (900 + θ) = Cos θ |
| cos (π/2 + θ) = – sin θ | Cos (900 + θ) = – Sin θ |
| tan (π/2 + θ) = -cot θ | Tan (900 + θ) = – Cot θ |
| cot (π/2 + θ) = -tan θ | Cot (900 + θ) = – Tan θ |
| sec (π/2 + θ) = -cosec θ | Sec (900 + θ) = – Cosec θ |
| cosec (π/2 + θ) = +sec θ | Cosec (900+θ) = Sec θ |
Shifting by π
| In radians | In degrees |
|---|---|
| sin (π + θ) = – sin θ | Sin (1800 + θ) = – Sin θ |
| cos (π + θ) = – cos θ | Cos (1800 + θ) = – Cos θ |
| tan (π + θ) = + tan θ | Tan (1800 + θ) = + Tan θ |
| cot (π + θ) = + cot θ | Cot (1800 + θ) = + Cot θ |
| sec (π + θ) = – sec θ | Sec (1800 + θ) = – Sec θ |
| cosec (π + θ) = – cosec θ | Cosec (1800+θ) = -Cosec θ |
Shifting by 2π
| In radians | In degrees |
|---|---|
| sin (2π + θ) = + sin θ | Sin (3600 + θ) = Sin θ |
| cos (2π + θ) = + cos θ | Cos (3600 + θ) = Cos θ |
| tan (2π + θ) = + tan θ | Tan (3600 + θ) = Tan θ |
| cot (2π + θ) = + cot θ | Cot (3600 + θ) = Cot θ |
| sec (2π + θ) = + sec θ | Sec (3600 + θ) = Sec θ |
| cosec (2π + θ) = + cosec θ | Cosec (3600+θ) = Cosec θ |
Other Periodicity equations
| In radians | In degrees |
|---|---|
| sin (π – θ) = +sin θ | Sin (1800 – θ) = Sin θ |
| cos (π – θ) = – cos θ | Cos (1800 – θ) = – Cos θ |
| tan (π – θ) = – tan θ | Tan (1800 – θ) = – Tan θ |
| cot (π – θ) = – cot θ | Cot (1800 – θ) = – Cot θ |
| sec (π – θ) = -sec θ | Sec (1800 – θ) = – Sec θ |
| cosec (π – θ) = + cosec θ | Cosec (1800-θ)= Cosec θ |
| In radians | In degrees |
|---|---|
| sin (3π/2 – θ) = – cos θ | Sin (2700 – θ) = – Cos θ |
| cos (3π/2 – θ) = – sin θ | Cos (2700 – θ) = – Sin θ |
| Tan (3π/2 – θ) = + Cot θ | Tan (2700 – θ) = + Cot θ |
| Cot (3π/2 – θ) = + Tan θ | Cot (2700 – θ) = + Tan θ |
| Sec (3π/2 – θ) = – Cosec θ | Sec (2700 – θ) = – Cosec θ |
| Cosec (3π/2 – θ)= -Sec θ | Cosec (2700-θ)= -Sec θ |
| In radians | In degrees |
|---|---|
| Sin (3π/2 + θ) = – Cos θ | Sin (2700 + θ) = – Cos θ |
| Cos (3π/2 + θ) = + Sin θ | Cos (2700 + θ) = + Sin θ |
| Tan (3π/2 + θ) = – Cot θ | Tan (2700 + θ) = – Cot θ |
| Cot (3π/2 + θ) = – Tan θ | Cot (2700 + θ) = – Tan θ |
| Sec (3π/2 + θ) = + Cosec θ | Sec (2700 + θ) = + Cosec θ |
| Cosec (3π/2 + θ) = – Sec θ | Cosec (2700+θ) = – Sec θ |
| In radians | In degrees |
|---|---|
| Sin (2π – θ) = – Sin θ | Sin (360 0 – θ) = – Sin θ |
| Cos (2π – θ) = + Cos θ | Cos (360 0 – θ) = + Cos θ |
| Tan (2π – θ) = – Tan θ | Tan (360 0 – θ) = – Tan θ |
| Cot (2π – θ) = – Cot θ | Cot (360 0 – θ) = – Cot θ |
| Sec (2π – θ) = + Sec θ | Sec (3600 – θ) = + Sec θ |
| Cosec (2π – θ)= – Cosec θ | Cosec (3600– θ)= – Cosec θ |
Even and Odd Angle Trigonometry Formula
• sin(−θ) = −sinθ • cos(−θ) = cosθ • tan(−θ) = −tanθ • cosec(−θ) = −cosecθ • sec(−θ) = secθ • cot(−θ) = −cot
Double Angle Trigonometry Formula
Here double angle means double of an angle. There are also Double Angle Formula in Trigonometry Formula, some of the major formulas are as follows-
• sin 2θ = 2 sin θ cos θ or (2 tan θ) / (1 + tan 2 θ)
• cos 2θ = cos²θ – sin²θ or 2cos 2 θ – 1 or 1 – 2sin 2 θ or (1 – tan 2 θ) / ( 1 + tan 2 θ)
• tan 2θ = 2 tan θ / (1 – tan²θ)
• cot 2θ = (cot²θ – 1) / 2 cot θ
• sec 2θ = sec 2 θ/2- sec 2 θ
• cosec 2θ = (secθ.cosecθ)/2
If the angles are tripled then the following formulas are obtained –
• sin 3θ = 3sin θ – 4sin 3 θ
• cos 3θ = 4cos 3 θ – 3cos θ
• tan 3θ = (3tan θ – tan 3 θ) / (1 – 3tan 2 θ)
• cos 3θ = (cos 3 θ – 3cos 3 θ)/( 3cos 2 θ -1)
Trigonometric identities of sum and difference of angles
• sin(A+B) = sin A . cos B + cos A . sin B
• cos (A+B) = cos A . cos B − sin A . sin B
• tan (A + B) = (tan A + tan B) / ( 1 − tan A . tan B)
• cot (A + B) = (cot A . cot B − 1) / (cot B + cot A)
• sin(A-B) = sin A . cos B − cos A . sin B
• cos (A-B) = cos A . cos B + sin A . sin B
• tan(A – B)= ( tan A – tan B )/ ( 1 + tan A . tan B )
• cot(A – B) = (cot A . cot B + 1) / ( cot B – cot A )
Product to Sum Identities
• 2sin A . sin B = cos(A – B) – cos(A + B)
• 2sin A . cos B = sin(A + B) + sin(A – B)
• 2cos A . sin B = sin(A + B) – sin(A – B)
• 2cos A . cos B = cos(A + B) + cos(A – B)
Sum to Product Identities
• sinA + sinB = 2[sin((A + B)/2)cos((A − B)/2)]
• sinA − sinB = 2[cos((A + B)/2)sin((A − B) /2)]
• cosA + cosB = 2[cos((A + B)/2)cos((A − B)/2)]
• cosA − cosB = −2[sin((A + B)/2)sin( (A − B)/2)]
Even Trigonometric Functions
A trigonometric function is said to be an even function if f(-x) = f(x).
• Sin (-x) = – Sin x
• Cos (-x) = Cos x
• Tan (-x) = -Tan x
• Cosec (-x) = – Cosec x
• Sec (-x) = Sec x
• Cot (-x) = -Cot x
Inverse Trigonometry Formulas
• sin -1 (-x) = -sin -1 x
• cos -1 (-x) = π – cos -1 x
• tan -1 (-x) = -tan -1 x
• cosec -1 (-x) = -cosec -1 x
• sec -1 (-x) = π – sec -1 x
• cot -1 (-x) = π – cot -1 x
Half angle identities
• Sin θ = 2 sin(θ/2) . cos(θ/2)
• Cos θ = [cos 2 (θ/2)- sin 2 (θ/2)]= [2 cos 2 (θ/2) – 1] = [1 – 2 sin 2 (θ/ 2)]
• cos θ = [{1- tan 2 (θ/2)}/ {1 + tan 2 (θ/2)}]
• tan θ = [{2 tan (θ/2)} / {1- tan 2 (θ/2)}]
• sin(A/2) = +/- √((1 – cos(A))/2)
• cos(A/2) = +/-√((1 + cos(A ))/2)
• tan(A/2) = +/- √((1 – cos(A))/(1 + cos(A))
Trigonometry Important Questions
Now we are going to solve some important questions based on the Trigonometry Formulas for Competitive Exams mentioned above. These questions are also important for SSC Exams.
Question 1. Find the values of tanA and cotC in the triangle given below.
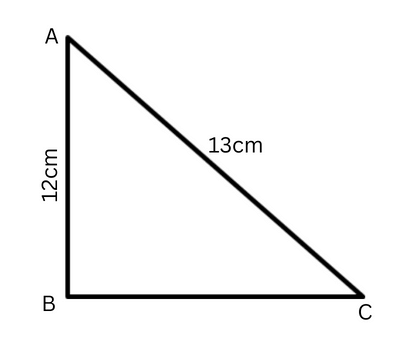
Solution- As in the given figure, the altitude of a right angled triangle is 12 cm and the hypotenuse is 13 cm. First of all, we will find the length of the base of the given triangle from Pythagoras theorem. Pythagoras theorem – AC2 = AB2 + BC2 BC2 = AC2 – AB2 BC2 = (13)2 – (12)2 = 169 – 144 = 25 Therefore, BC = 5 cm Now according to Trigonometry Formula tan A = perpendicular / base = BC/AB = 5/12 and cot C = base / perpendicular = BC/AB = 5/12
Question-2 : If A, B and C are the interior angles of a triangle ABC, then prove that sin (B + C/2) = cos A/2.
Solution - We know that for a given triangle, the sum of all the interior angles of the triangle is equal to 180°. Therefore A + B + C = 180° or B + C = 180° – A Dividing both sides by 2 ⇒ (B + C)/2 = (180° – A)/2 ⇒ (B + C)/2 = 90° – A/2 Taking sin on both sides- sin (B + C)/2 = sin (90° – A/2) ⇒ sin (B + C)/2 = cos A/2 (according to the Trigonometry Formula sin(90° – θ) = cos θ)) Proved.
Question-3 – If sin 3A = cos (A – 26°), where 3A is an acute angle, then find the value of angle A.
Solution: Given- sin 3A = cos(A – 26°); where 3A is an acute angle. or cos(90° – 3A) = cos(A – 26°) (according to Trigonometry Formula cos(90° – θ) = sin θ) ⇒ 90° – 3A = A – 26 ⇒ 3A + A = 90° + 26° ⇒ 4A = 116° ⇒ A = 116°/4 ⇒ A = 29° Answer- Angle A = 29°
Question -4- If tan(A + B) = √3 and tan(A – B) = 1/√3 ; 0° < A + B ≤ 90°; A > B, then find the value of A and B.
Solution- Given that- tan(A + B) = √3 or tan(A + B) = tan 60° (since tan 60° = √3 ) Hence A + B = 60°………. Equation (i) And tan(A – B) = 1/√3 or tan(A – B) = tan 30° (since tan 30° = 1/√3 ) Hence A – B = 30°….……. Equation (ii) Addition of equation (i) and (ii)- A + B + A – B = 60° + 30° 2A = 90° A = 45° Now put this value of A in equation (i)- 45° + B = 60° B = 60° – 45° = 15° Thus angle A = 45° and angle B = 15°
Question-5- If tan θ + sec θ = m, then prove that sec θ = (m 2 + 1)/2m
Solution-
Given that –
tan θ + sec θ = m…………Equation(i)
We know that-
sec2θ – tan2θ = 1
(sec θ – tan θ)(sec θ + tan θ) = 1 {According to Formula a 2 – b 2 = (a – b)(a + b)}
(sec θ – tan θ) m = 1 (from equation (i))
sec θ – tan θ = 1/m………Equation (ii)
Adding equation (i) and (ii) -
tan θ + sec θ + sec θ – tan θ = m + (1/m)
2 sec θ = (m2 + 1)/m
sec θ = (m2 + 1)/2m
So proved.Question – 6- If a sin θ + b cos θ = c, then prove that a cos θ – b sin θ = √(a 2 + b 2 – c 2 ).
Solution: Given that- a sin θ + b cos θ = c Square both the sides, (a sin θ + b cos θ)2 = c2 a2 sin2θ + b2 cos2θ + 2ab sin θ cos θ = c2 We know that sin2A + cos2A = 1 or sin2 A = 1 - cos2 A and cos2 A = 1 - sin2 A Therefore- a2(1 – cos2θ) + b2(1 – sin2θ) + 2ab sin θ cos θ = c2 ⇒ a2 – a2 cos2θ + b2 – b2 sin2θ + 2ab sin θ cos θ = c2 ⇒ a2 + b2 – c2 = a2 cos2θ + b2 sin2θ – 2ab sin θ cos θ ⇒ a2 + b2 – c2 = (a cos θ – b sin θ)2 ⇒ a cos θ – b sin θ = √(a2 + b2 – c2) Hence proved.
Question – 7- In a triangle ∆ ABC, angle B is right angled, and AB = 24 cm, BC = 7 cm then find the values of sin A, sin C, cos A and cos C.
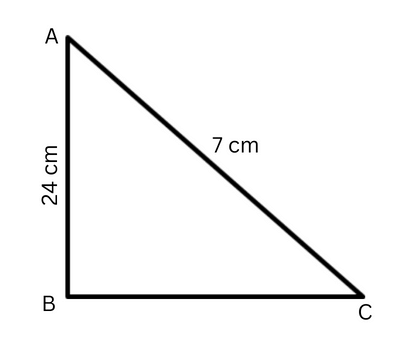
Solution- In the given right triangle, B = 90°. then AC2 = AB2 + BC2 AC2 = (24)2 + 72 AC2 = (576 + 49) AC2 = 625 cm2 AC = 25 cm Therefore Sin A = perpendicular / hypotenuse = 7/25 cos A = base/hypotenuse = AB/AC = 24/25 Sin C = perpendicular / hypotenuse = AB/AC = 24/25 Cos C = base/hypotenuse = BC/AC = 7/25
Question 8: If Sin A = 3/4 then find the values of cos A and tan A.
Solution: Let ABC be a right triangle and angle B = 90 0 . It is given that Sin A = 3/4 Since, Sin A = perpendicular/diagonal = 3/4 So according to Pythagoras theorem base2 = 42 – 32 Let 16 – 9 = 7 Base = √7 So cos A = √7 /4 And tan A = 3/√7
Question 9: In a triangle, if ∠A and ∠B are acute angles and cos A = cos B, then prove that ∠ A = ∠ B.
Solution: Let angle C be right angled in triangle ABC, then cos A = AC/AB cos B = BC/AB Since it is given that cos A = cos B then AC/AB = BC/AB AC = BC This proves that triangle ABC is an isosceles triangle and by the definition of an isosceles triangle, the angles opposite to two equal sides are equal. Therefore ∠A = ∠B Hence Proved.
Question 10: In a triangle PQR, angle Q is right angled such that PR + QR = 25 cm and PQ = 5 cm. Then find the values of sin P, cos P and tan P.
Solution: It is given that in a triangle PQR, PQ = 5 cm and PR + QR = 25 cm. Let QR = x cm Then PR = 25 – QR = 25 – x So according to Pythagoras theorem PR2 = PQ2 + QR2 Putting the values of PR, PQ and QR- (25 – x)2 = (5)2 + (x)2 252 + x2 – 50x = 25 + x2 625 – 50x = 25 50x = 600 x = 12 So, QR = 12 cm PR = 25 – QR = 25 – 12 = 13 cm So, sin P = QR/PR = 12/13 cos P = PQ/PR = 5/13 then P = QR/PQ = 12/5
Question 11 : Find the value of 2tan245° + cos230° – sin260°
Solution: From the above Trigonometry table- tan 45° = 1 cos 30° = √3/2 sin 60° = √3/2 Therefore, putting their values in the equation given in the question- 2(1)2 + (√3/2)2 – (√3/2)2 = 2 + 0 = 2
Question 12 : If tan (A + B) =√3 and tan (A – B) =1/√3, where 0° < A + B ≤ 90°; A > B, then find the value of A and B.
Solution: Given that- tan (A + B) = √3 and tan (A – B) =1/√3 From Trigonometry Table, tan 60° = √3 and tan 30° = 1/√3 tan (A + B) = √3 ⇒ tan (A + B) = tan 60° ⇒ (A + B) = 60° …………… equation (i) And tan (A – B) = 1/√3 ⇒ tan (A – B) = tan 30° ⇒ (A – B) = 30° ..... Equation (ii) Adding equation (i) and (ii)- A + B + A – B = 60° + 30° 2A = 90° A= 45° Now putting the value of A in equation (i) 45° + B = 60° B = 60° – 45° B = 15° Therefore, A = 45° and B = 15°
Question 13 : Prove that: (i) tan 48° tan 23° tan 42° tan 67° = 1 (ii) cos 38° cos 52° – sin 38° sin 52° = 0
Solution:
(i) in tan 48° tan 23° tan 42° tan 67°
tan 48° = tan(90° – 42°) = cot 42° {since cot θ = tan (90° – θ)}
and tan 23° = tan (90° – 67°) = cot 67°
Therefore
tan 48° tan 23° tan 42° tan 67°
= cot 42° cot 67° tan 42° tan 67°
= (cot 42° tan 42°) (cot 67° tan 67°)
= 1 × 1 [since cot A.tan A = 1]
= 1
(ii) in cos 38° cos 52° – sin 38° sin 52°
cos 38° = cos (90° – 52°) = sin 52° {since sin θ = cos(90° – θ)}
And
cos 52°= cos (90° – 38°) = sin 38°
Therefore
sin 52° sin 38° – sin 38° sin 52° = 0Question 14 : If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution: Given that- tan 2A = cot (A – 18°) according to the trigonometric identity tan 2A = cot (90° – 2A) Putting this in the given equation cot (90° – 2A) = cot (A – 18°) hence - 90° – 2A = A – 18° 108° = 3A A = 108° / 3 Therefore A = 36°
Question 15 : If A, B and C are the interior angles of a triangle ABC, then prove that sin [(B + C)/2] = cos A/2
Solution: As we know that the sum of all the three interior angles of a triangle is 180°. Therefore, A + B + C = 180°……. Equation (i) Or B + C = 180° – A Now dividing by 2 on both sides- ⇒ (B + C)/2 = (180° – A)/2 ⇒ (B + C)/2 = 90° – A/2 Now taking sin on both sides ⇒ sin (B + C)/2 = sin (90° – A/2) or sin (B + C)/2 = cos A/2 (since sin(90°- θ) = cos θ)
FAQs related to Trigonometry Formulas for Competitive Exams
What is sine, cosine and tangent of an angle in trigonometry?
The sine of an angle of a right triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
While the cosine of that angle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse and the tangent of the angle is the ratio of sine to cosine.
How many types of Trigonometric Ratio are there?
There are 6 types of trigonometric ratios – Sine, Cosine, Tangent, Co-secant, Secant and Co-tangent.
Their abbreviated forms are – sin, cos, tan, cosec, sec and cot.
What is Pythagorean theorem in trigonometry?
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
If the hypotenuse is c and the other two sides are a and b, then by the Pythagorean theorem c2 = a2 + b2 .
In trigonometry, this theorem is often used to find the length of a side of a right triangle.
What is the double angle formula for sine, cosine, and tangent in trigonometry?
In trigonometry, double angle formulas are used to find the sine, cosine, or tangent of double an angle.
The double angle formulas are:
sin(2A) = 2sin(A)cos(A)
cos(2A) = cos2 (A) – sin2 (A) = 2cos2 (A) – 1 = 1 – 2sin2 (A)
tan(2A) = 2tan(A)/(1 – tan2 (A))
What is the half angle formula for sine, cosine, and tangent in trigonometry?
In trigonometry, half angle formulas are used to find the sine, cosine, or tangent of half of an angle.
The half angle formulas are as follows:
sin(A/2) = ±√[(1 – cos A) / 2]
cos(A/2) = ±√[(1 + cos A) / 2]
tan(A/2 ) = ±√[1 – cos A] / [1 + cos A] or sin A / (1 + cos A) (or) (1 – cos A) / sin A
What are some important Trigonometric Identities?
Some important trigonometric equations are-
sin²θ + cos²θ = 1
sin²θ = 1 – cos²θ
cos²θ = 1- sin²θ
sec²θ – tan²θ = 1
1 + tan²θ = sec²θ
sec²θ –1 = tan²θ
cosec²θ = cot²θ + 1
sinθ = √(1 – cos²θ)
cosθ = √( sinθ – 1 )
tan²θ = sec²θ – 1
tanθ = √(sec²θ – 1)
secθ = √(1 + tan²θ)
cosecθ = √(cot²θ + 1)
cot²θ = cosec²θ – 1
cot²θ = √(cosec²θ – 1)



